What Is Directed Graph

TL;DR

In the previous post, we recapped some of the oldest software testing definitions. Today we introduce Directed Graphs that are an important foundation for many test coverage criteria. We will introduce you to software testing based on the remarkable book,  Introduction To Software Testing by Paul Ammann and Jeff Offutt.

Directed Graph Models

Based on the artifact under test, we create a directed graph model of that artifact. Remember that all models are wrong, but some are useful. Directed Graph models are our abstractions of those artifacts. We could also create several different directed graph abstractions for the same artifact. The most known directed graph is for artifact source code control flow statements. We create artifact test cases based on directed graph paths.

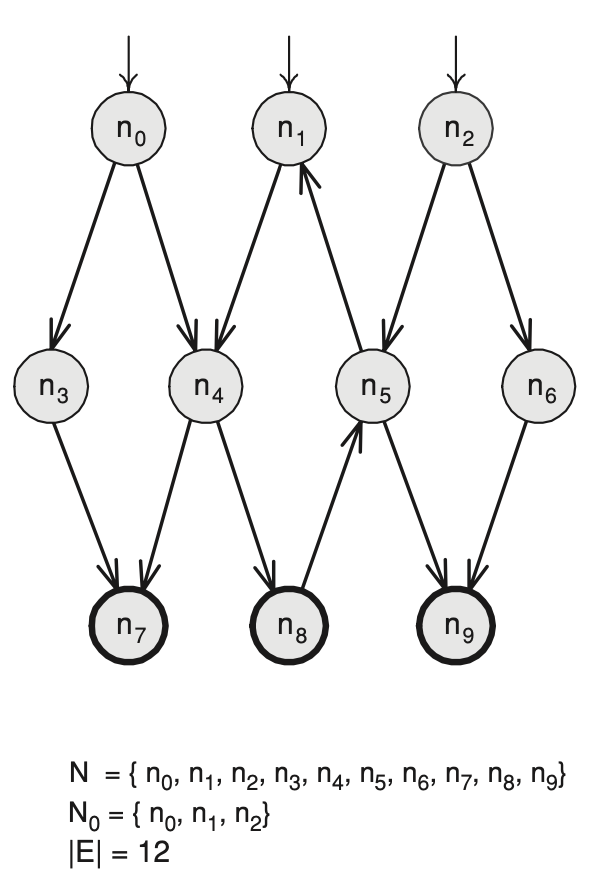
Directed Graph

The above image is how we usually draw a directed graph, using circles for nodes and arrows for edges.  Here is how we use mathematic to note a directed graph:

• A graph is noted with G
• A set of nodes N = { n0, n1, n2, n3, ..., n9 }
• A set of initial nodes N0 = { n0, n1, n2 }
• A set of final nodes Nf = { n7, n8, n9 }
• A set of edges where the edge is a path between two nodes. We have 12 edges, E = | 12 |. E = { (n0, n3), (n0, n4), (n3, n7), (n4, n7), (n1, n4), (n4, n8), (n8, n5), (n5, n1), (n2, n5), (n2, n6), (n5, n9), (n6, n9) }

Initial and final nodes represent the initial and final state of the artifact under test. Note that an interesting path is a path that starts from initial nodes but does not end in a final node. Also, the task for noting all the edges is a perfect automation opportunity.

Path

The path is a sequence of nodes and edges where nodes are connected with an edge. The path length is the number of edges in that sequence.

Node Reachability

We say that node n is reachable from a node n0 if there is a path between those two nodes.

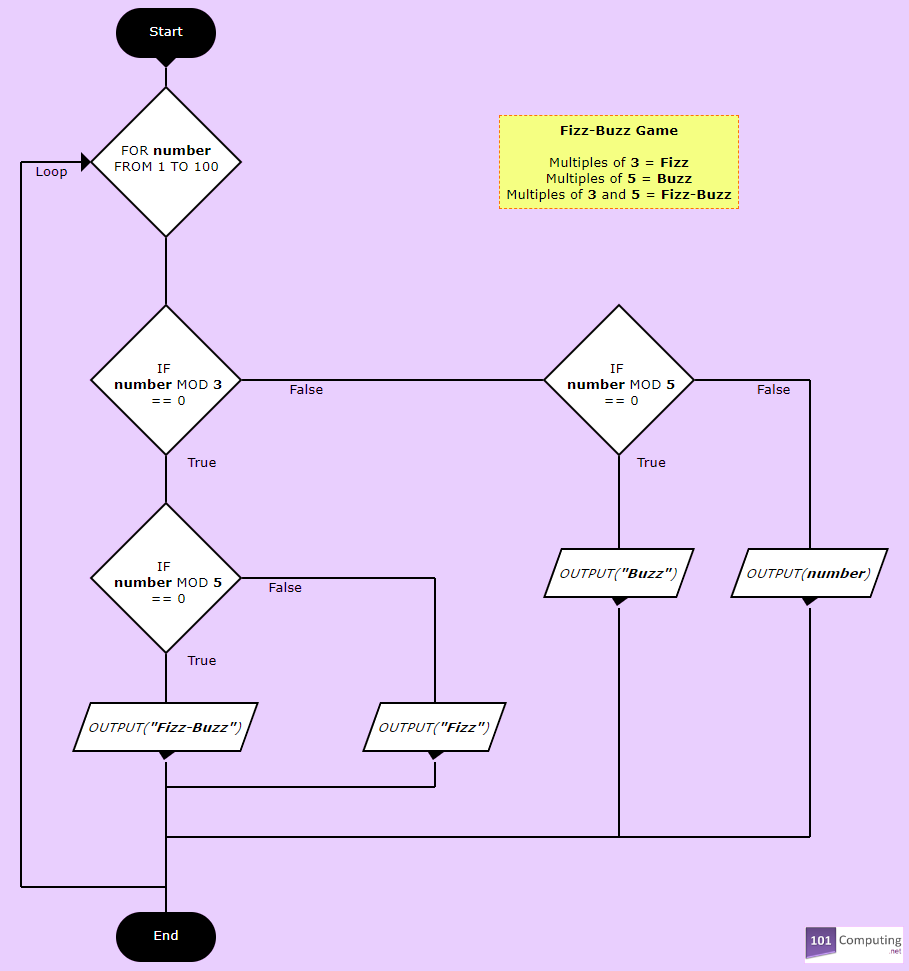
Fizz Buzz Algorithm

Let’s make a directed graph for Fizz-Buzz Algorithm.

For this challenge, you need to write a computer program that will display all the numbers between 1 and 100.

For each number divisible by three, the computer will display the word “fizz,”
For each number divisible by five, the computer will display the word “buzz,”
For each number divisible by three and five, the computer will display the word “fizz-buzz.”

We have 10 nodes and 12 edges. But how many paths?