TL;DR

The disadvantage of fix-point decimal number representation is a limited number of significant digits that we can store in memory. That implies that we lose precision. Let’s examine floating-point number representation. The post is aligned with the Black Box Software Testing Foundations course (BBST) designed by Rebecca Fiedler, Cem Kaner, and James Bach.

Floating-point decimal number representation provides more precision but requires more computational power to calculate the actual stored value. This is why modern processors have co-processor that only does floating number calculations.

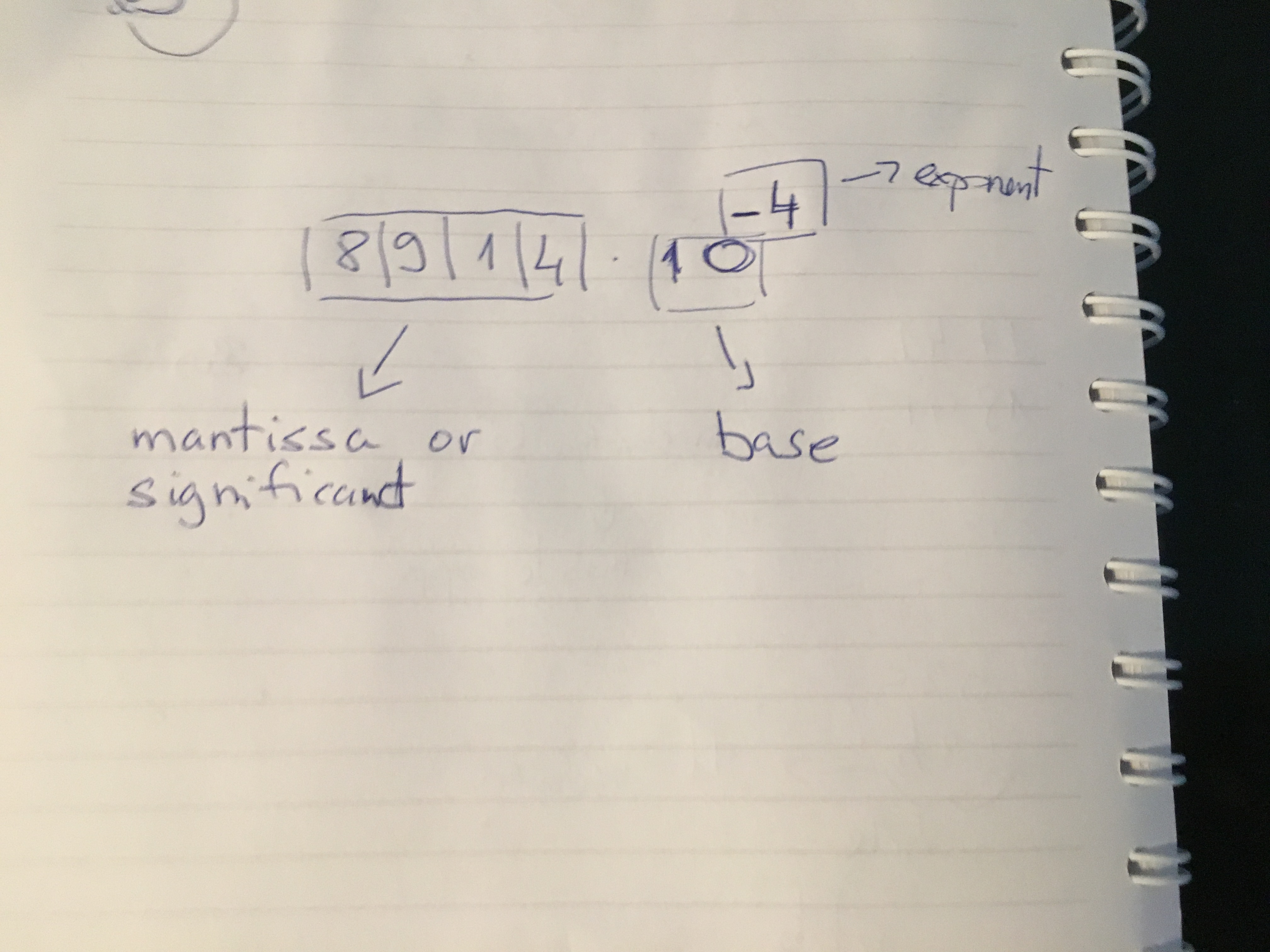
In the above picture, we can see that the floating-point number has the following components:

• mantissa or significant digits
• exponent
• base

It is a convention to show floating-point number with a decimal point after the most significant digit:

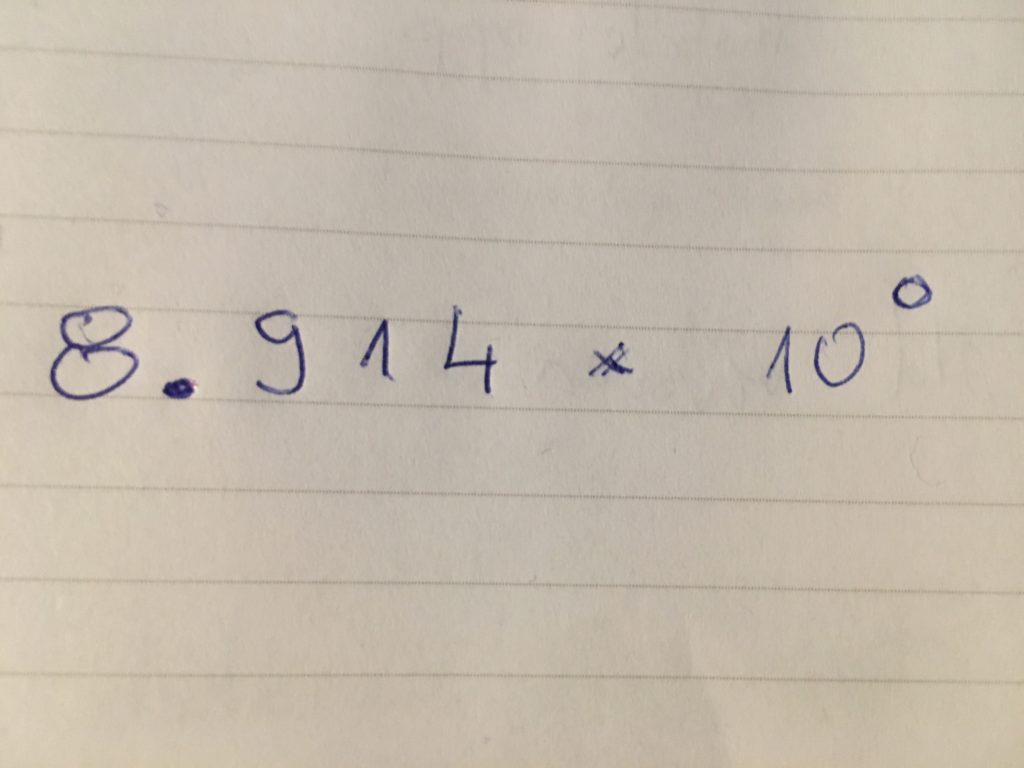
Overflow

The overflow happens when the result has more mantissa digits than we can store into boxes (memory):

What computer would do in this case is round down:

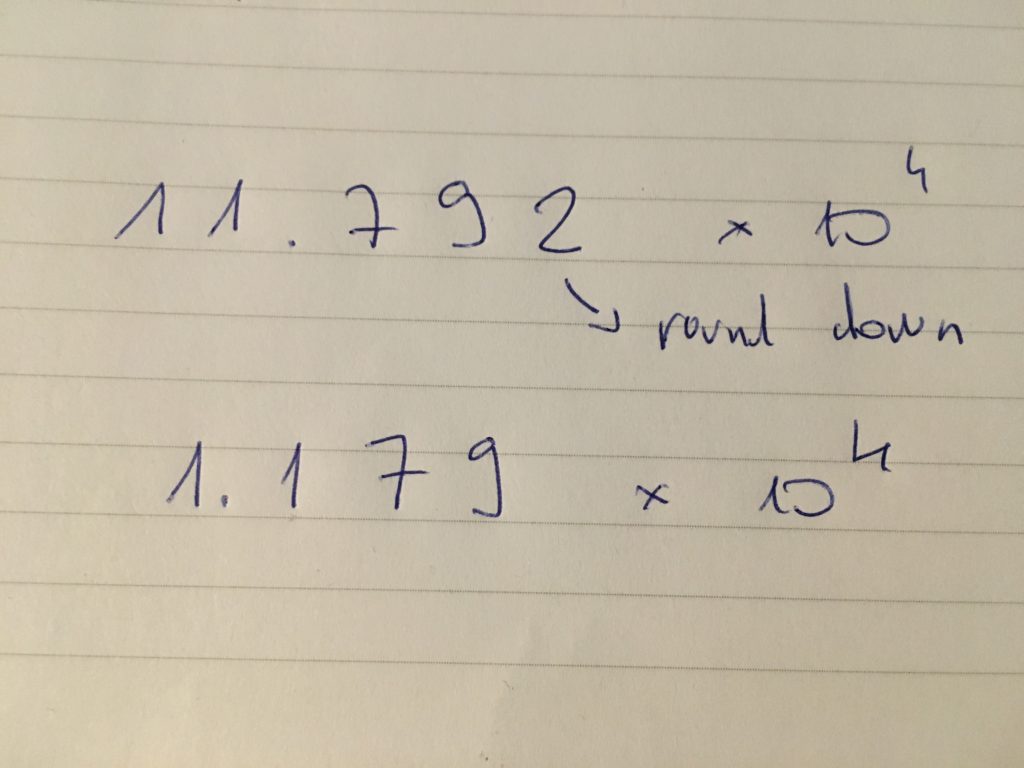
We need to store in computer memory all three parts of floating-point number:

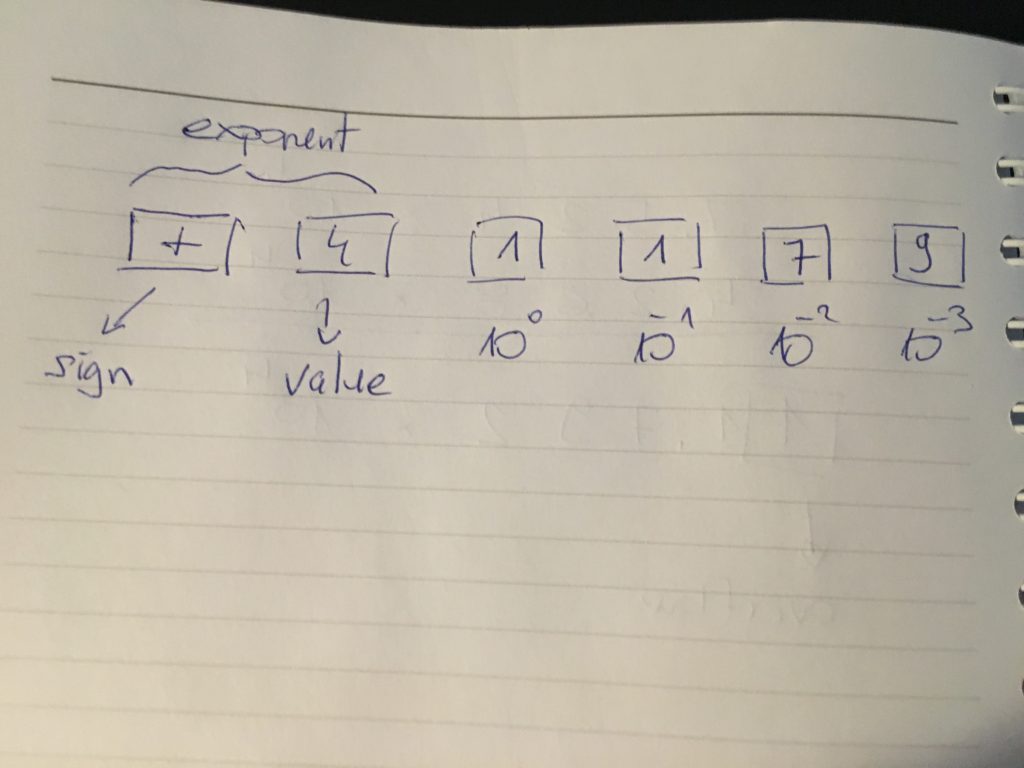
For exercise, what are the largest and smallest numbers that we can represent using floating-number representation from the picture above? Put your answer in a comment below.

More exercise. How would computer store following numbers using floating-point representation from above picture:

555511111.0

555599999.9

555501234.5

Which error is more significant, saying that 3.001 is 3.000 or saying that 2.99997 is 3.000?

What is the sum of:

1.234 x 10^10

1.234 x 10^-3

What is the product of 5.768 x 10^-3 and 4?

So if we want more precision for floating-point number representation, we must increase the number of digits for:

• mantissa
• exponent